Southeast Winds and Flooding from Continental Storms

Posted on December 19, 2022 by Philip Orton

A massive extratropical storm over the Midwest will bring strong southeast winds to New York Bight and the potential for widespread coastal flooding this Thursday and Friday. Sustained winds in the New York metro area will peak at 25-35 mph and rainfall will total 1-2 inches. The storm will intensify and sit over the Midwest Thursday and Friday before moving northward Friday so that winds will shift to come from the south and then west, bringing an extremely cold air mass into our area.

The Stevens Flood Advisory System (http://stevens.edu/SFAS) provides forecasts for the NY/NJ Harbor region with detailed coastal ocean and river models and an ensemble of storm data from the US, European and Canadian models. Given the coincidence of spring tides plus storm surge, there is a significant risk of coastal flooding for our region Thursday evening through Friday morning. On Friday morning’s high tide, there is potential for moderate coastal flood thresholds to be exceeded at all harbor regions and even major flood thresholds in the lowest-lying areas. Peak storm surge across the area is predicted to be 2-5 feet within 90% confidence. Central forecasts for peak water levels are forecast to be 5.0 feet NAVD88 for Battery (Figure 1) and 5.6.feet at Jamaica Bay (Figure 2). The near-worst-case scenarios (95th-percentile) are 6.2 feet and 6.7 feet, respectively, a National Weather Service designated “moderate flood” at New York Harbor and “major flood” for Jamaica Bay and some other low-lying areas.

We are normally concerned with nor’easter storms for coastal flooding impacts in our area, but the worst historical cool-season storm surge event came on a continental storm on November 25th 1950. That storm also caused southeast winds, but at speeds approaching hurricane strength. It caused a storm surge of 7.9 feet which peaked near the time of low tide, sparing most areas of severe flooding. During the typical rapid passage of a severe storm (12 hours or less), winds from the southeast have more efficacy in creating a large storm surge in New York Bight.

Figure 1:  Forecast water levels (top) and storm surge (bottom) at The Battery, Manhattan

Figure 2:  Forecast water levels (top) and storm surge (bottom) at Bergen Basin, Queens (near Kennedy Airport and Howard Beach)

Posted in security, water, weather | Tagged , , , , , , , | Leave a comment

Lessons on Containment for the Climate Pandemic

Posted on July 18, 2020 by Philip Orton

In the month of March, COVID19 deaths nationwide grew exponentially, at 20-30 percent per day, leading to a doubling every 3 days.  New Columbia University modeling shows the benefit of heeding scientific warnings early and using containment measures to stem a problem with explosive growth like COVID-19.  If social distancing and other containment measures were instituted in New York City just two weeks earlier, there would have been 94% fewer deaths.

Look closer at the numbers, and you’ll see how climate change and COVID19 are similarly explosive problems (see Figure below), with similar dangers from missing the opportunity for containment.  One silver lining is that the pandemic has led us to change our lives in some ways that could be made permanent, to simultaneously rein in climate change.

covid19-log

inwood-log

Figure:  (top) US daily COVID-19 deaths from late February to early May, and (bottom) floods per year caused by global sea level rise for Hamilton Beach, Queens, based on the water level that begins flooding streets there (7.1 feet above normal low tide).

Scientists have warned for decades of the catastrophic future effects of global warming; yet with little action to reduce carbon emissions since then, today we are experiencing a global average temperature of about two degrees Fahrenheit higher than it was in 1880 during the pre-industrial era.  We are actually fortunate that 90 percent of the heat has actually been absorbed by the ocean instead of warming the atmosphere.  However, the result of this is slowly-building, but accelerating, sea level rise.

As a result, many locations are seeing exponential growth of the number of floods per year, leading to calls for massive, expensive projects to avoid becoming uninhabitable.  For example, in some neighborhoods of Charleston, Atlantic City, and New York City — in the latter case the Hamilton Beach neighborhood near the John F. Kennedy International Airport— we used to see sporadic, occasional floods, but now these are happening about 40-60 times per year (see Figure).  These locations that have frequent nuisance flooding today are unusually low-lying neighborhoods built on landfill over wetlands.

HowardBeach-MBC_2

Photograph showing Hamilton Beach, New York City, “sunny day” flooding for a water level of 7.3 feet above normal low tide, May 15, 2019.

Within a few decades rising sea levels will cause neighborhoods at higher elevations to be similarly affected with chronic flooding, affecting property valuing in the trillions of dollars.  For example, my research with the New York City Panel on Climate Change has shown that within the city today, chronic tidal flooding affects streets where 1700 people reside. In the 2050s this could rise to 34000 people, and by 2100 it could rise to 750,000 people, if the Antarctic ice sheet begins to collapse and dramatically increase sea level rise.

Unchecked, COVID19 had a doubling time of days, and one might be comforted by the fact that floods are doubling much more slowly, every decade or so.  However, there is another critical difference:  The ramp-up time for containment activities for COVID-19 was weeks-to-months, with testing and contact tracing.  The ramp-up time for alternative energy sources to replace fossil fuels is decades.  If we fail to stop emissions rapidly, there is wide agreement that the consequences will be devastating – eventually sea level rise of several feet will require retreat from the rising ocean.

A wise recovery plan from the pandemic will help address both of these explosive problems.  For example, businesses can create permanent policies that encourage more work from home and less automobile and airplane travel, reducing carbon dioxide emissions from transportation that are a major contributor to global warming; some are finding this actually enhances productivity.  Going further, long-term policies can promote smaller offices with fewer on-site employees, reducing the need for office space that is empty a majority of the time – building energy is also a top source of emissions. Cities could become more livable, with more empty building space available to create housing.

One of the most profound lessons taught by our virus response is that we are all capable of transformative change.  The only long-term solution for containment of the climate pandemic is to eliminate carbon dioxide emissions, and now that we’ve taken steps in the right direction, we should avoid backtracking to business-as-usual.

 

Posted in climate, opinion, water | Tagged , , , , , , , , , , , , , , , | Comments Off on Lessons on Containment for the Climate Pandemic

Vanishing Glaciers, Rising Seas, and More Street Flooding in Low-Lying New York City Neighborhoods

Posted on October 1, 2019 by Philip Orton

A guest post by Dr. Vivien Gornitz

 

The Okjokull glacier in Iceland is no more.

In 2014, Oddur Sigurosson, a prominent Icelandic glaciologist, declared that the remnant ice was too thin to qualify as a glacier. A plaque erected to mark its demise warned that “In the next 200 years all our glaciers are expected to follow the same path.”

This summer, the world endured the hottest July ever.  The Arctic, in particular, is warming twice as fast as the rest of the world. Alaska baked under record July heat.  The intense heat that had gripped several European countries a week earlier reached Greenland between July 29-30 and August 3, 2019, where about 90 percent of its icy surface melted, including the summit of the ice sheet.  Twelve and a half billion tons melted on August 2–the largest single-day meltdown ever! In 2019 to date, the Greenland Ice Sheet shed a total ice mass rivaling that of 2012, the current record-setting year.

Thawing glaciers and ice sheets now account for nearly two thirds of the present global sea level rise (SLR) of 3 mm/yr.  Ice attrition on mountain glaciers grew from the sea level rise equivalent of 0.2 to 0.3 mm/yr in the 1980s to nearly 1 mm/yr between 2011 and 2016.  Greenland added ~0.13 mm/yr to the oceans prior to 2000, going to ~0.7-0.8 since 2010.  The awakening giant, Antarctica, nearly quadrupled its sea level contribution since the 2000s.

The thawing ice sheets raise additional concerns.  Much of the West Antarctic Ice Sheet (WAIS) is potentially unstable because it lies on bedrock largely grounded[1] below sea level.  As ocean water warms, it will melt the undersides of floating ice shelves and weaken their ability to buttress grounded ice. Eventually, this could trigger a Marine Ice Sheet Instability (MISI) on marine-terminating glaciers whose beds tilt landward.  Once initiated, the grounding line continues to retreat landward until the glacier bed slope levels off.  Atmospheric warming and hydrofracturing would further hasten ice shelf breakup, leading to collapse of high ice cliffs (≥100 m above water). A number of WAIS ice shelves are already thinning and glacier grounding lines are in retreat.

Increased ice melting, as well as potential ice sheet instabilities, raise prospects of higher than previously anticipated sea level.  More frequent coastal flooding due to the higher waters would endanger people and structures in low-lying areas, worldwide.  Coastal managers and decision-makers should therefore consider the design and construction of urban infrastructure and transportation networks that can withstand rare long-range, although high consequence events, as well as ones more likely to occur.

These considerations motivated the New York City Panel on Climate Change (NPCC), an advisory team of academic and private-sector experts, to introduce a physically-plausible end of century extreme, though low probability, sea level rise scenario for New York City.  The ARIM (Antarctic Rapid Ice Melt) scenario includes the possibility of future Antarctic ice sheet destabilization, particularly under high carbon-emissions futures. ARIM focuses on a narrow subset of high sea levels based on the ‘Extreme’ SLR scenario from a recent national climate assessment, as well as several other recent publications.

Rockaway Peninsula during a small storm surge with high spring tides (credit: Gilles Ashford)

Up to the 2050s, the ARIM scenario closely resembles prior results from a 2015 NPCC report.  However, by the 2080s, ARIM projects a 2.1 m sea level rise, climbing to 2.9 m by 2100.  This contrasts with a SLR of 1.5 m by the 2080s and 1.9 m by 2100 at the 90th percentile in the NPCC (2015) report. (Note, however, that the NPCC (2015) projections still remain the scientific basis of New York City resiliency planning).

Higher sea levels and increasing coastal flood exposure pose growing challenges for the large population and major economic assets along New York City’s shoreline. Historically, the city has been struck by a number of severe coastal floods (both hurricanes and nor’easters). Superstorm Sandy in 2012 generated the highest water levels in at least 300 years and caused an estimated $19 billion in damages and 43 fatalities in the city. But major coastal storms are not the only hazard of rising seas.

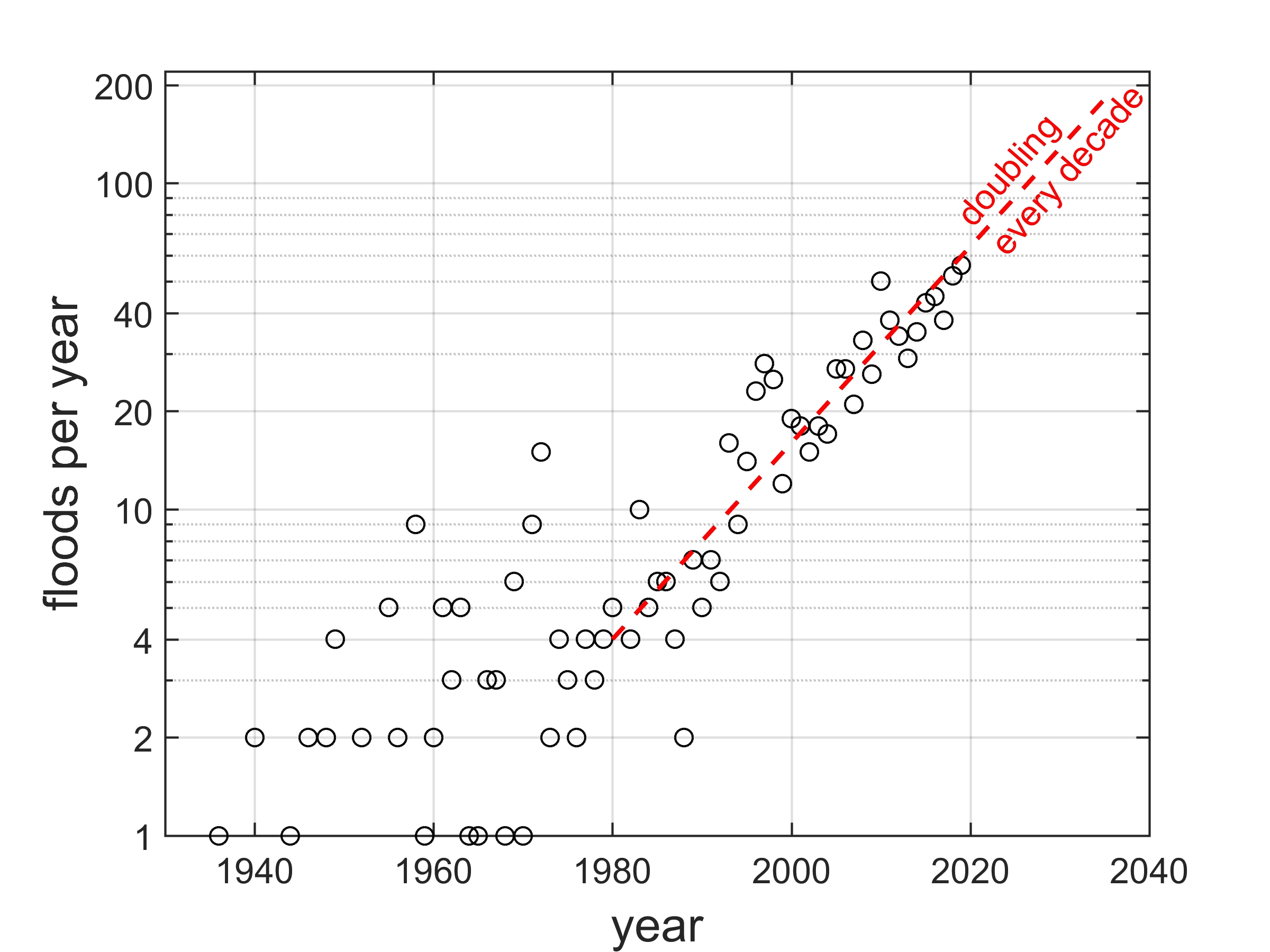
An early manifestation of SLR is the increasing incidence of clear weather “nuisance flooding”, or tidally related flooding of streets, basements, and low-elevation highways. The number of such incidents has increased substantially in the United States since the 1950s. Sections of several low-lying neighborhoods surrounding Jamaica Bay and Rockaway Peninsula already experience frequent nuisance flooding (see photo above).

 

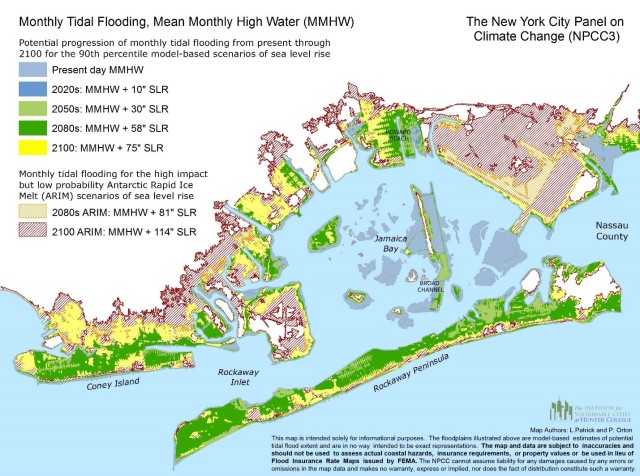
Figure 1.  Future growth of the area affected by monthly tidal flooding around Jamaica Bay, Coney Island, and the Rockaways, New York City, for NPCC (2015) 90th percentile and ARIM SLR scenarios. Results assume no future shoreline changes due either to coastal erosion or coastal flood protection, and may therefore under- or overestimate flood area. Because of remaining uncertainties associated with ARIM, this map is not intended for planning purposes.

 

A worst-case sea level rise scenario such as ARIM would not only increase coastal flood levels, but would also lead to a progressive landward expansion of the floodplain over time (Fig. 1).  Under ARIM, monthly tides would flood a much broader area than under the 90th percentile NPCC (2015) projections, over the same time periods. Moreover, neighborhoods around Jamaica Bay, previously exposed to frequent tidal flooding could become permanently submerged by late century, without strengthened coastal protection. Several other city waterfront communities face a similar risk.

Guided by NPCC findings, New York City undertakes programs to strengthen local coastal defenses tailored to specific neighborhood needs.  Examples include installation of temporary or permanent barriers (such as a floodwall or berm), raising bulkheads, seawalls, and building neighborhood-scale levees and storm surge barriers.  Plans have been proposed to raise streets subject to frequent nuisance flooding.  Nevertheless, extensive high density development is occurring close to the waterfront within the present-day 100-year flood zone. Long-term planning should therefore include more sustainable land-use zoning to minimize or avoid high-density development in flood-prone areas and preserve natural vegetation, such as salt marshes, as buffer zones against high waves.

Will even these resiliency measures suffice in light of a potential high-end sea level future?  Will managed relocation of the most vulnerable neighborhoods ultimately become a necessity? The consequences of substantial potential future economic and societal disruptions from low probability, yet high consequence events in major coastal urban centers such as New York City, highlight the urgency of investigating upper-end sea level scenarios for long-term coastal risk management.

 

[1] Ice resting on bedrock. The grounding line delineates the boundary between land-based ice and an attached floating ice shelf.

 

Further reading

Bamber, J.I., Westaway, R.M., Marzeion, B., and Wouters, W., 2018. The land ice contribution to sea level during the satellite era. Environmental Research Letters, 13:063008, https://doi.org/10.1088/1748-9326/aac2f0

Gornitz, V., Oppenheimer, M., Kopp, R., Orton, P., Buchanan, M., Lin, N., Horton, R., and Bader, D., 2019: New York City Panel on Climate Change 2019 Report. Chapter 3. Sea level rise. In:  Advancing Tools and Methods for Flexible Adaptation Pathways and Science Policy Integration. Rosenzweig C, Solecki W (eds). Ann. New York Acad. Sci. 1439: 71-94.

Gornitz, V., 2019. Vanishing Ice: Glaciers, Ice Sheets and Rising Seas. New York, NY: Columbia University Press.

Holson, L.M., Iceland mourns loss of a glacier by posting a warning about climate change. New York Times, August, 19, 2019. https://www.nytimes.com/2019/08/19/world/europe/iceland-glacier-funeral.html

Horton, R., Little, C., Gornitz, V., Bader, D., and Oppenheimer, M., 2015: Chapter 2. Sea level rise and coastal storms. In: New York City Panel on Climate Change 2015 Report: Building the Knowledge Base for Climate Resiliency, Rosenzweig C, Solecki W (eds). Ann. New York Acad. Sci., 1336, 36-55.

Ilyushina, M. and Pleitgen, F., 2019. At the bottom of a glacier in Greenland, scientists find troubling signs. CNN.  https://www.cnn.com/2019/08/19/weather/greenland-nasa-climate-battle-intl/index.html (updated Aug. 20, 2019).

Michaels, M., 2019.A closer look at the heat that smashed all-time records in Alaska. Weather Nation.  https://www.weathernationtv.com/news/a-closer-look-at-the-heat-that-smashed-all-time-records-in-alaska/ (posted July 22, 2019).

Orton, P., Lin, N., Gornitz, V., Colle, B., Booth, J., Feng, K., Buchanan, M., Oppenheimer, M., and Patrick, L., New York City Panel on Climate Change 2019 Report. Chapter 4. Coastal Flooding. In:  Advancing Tools and Methods for Flexible Adaptation Pathways and Science Policy Integration. Rosenzweig C, Solecki W (eds). Ann. New York Acad. Sci. 1439:95-114.

Rignot, E., Mouginot, J., Scheuchl, B., van den Broeke, M., van Wessem, M.J., and Morlighem, M., 2019. Four decades of Antarctic Ice Sheet mass balance from 1979-2017. Proc. Natl. Acad. Sciences 116(4):1095-1103.

Scambos, T., et al., 2019. Europe’s warm air spikes Greenland melting to record levels. NSIDC, Greenland Ice Sheet Today. http://nsidc.org/greenland-today/2019/08/europes-warm-air-spikes-greenland-melting-to-record-levels/ (posted Aug. 6, 2019).

Zemp, M., et al., 2019. Global glacier mass changes and their contributions to sea level rise from 1961 to 2016. Nature. https://doi.org/10.1038/s41586-019-1071-0

 

Posted in climate, water | Tagged , , , , , , , , , , | Comments Off on Vanishing Glaciers, Rising Seas, and More Street Flooding in Low-Lying New York City Neighborhoods

Pants on Fire, Causing Higher Carbon Emissions

Posted on July 9, 2019 by Philip Orton

President Trump, concerned about poor performance with Millennials and Independents is now touting his record in reducing US carbon emissions.  This Pants-On-Fire lie has him taking credit for a decade-long trajectory toward lower emissions that is predominantly caused by a shift from one fossil fuel (coal) to another (natural gas).  His role in emissions from 2017-2018 is minimal, as carbon emissions respond very slowly to policy changes — consider when emissions change when a auto emissions policy is put into place, or power plant policy change is made – years to decades into the future.

Most importantly, in judging Trumps’ actual performance on dealing with climate change, is that the Trump administration cannot point to a single policy change that will reduce future emissions.

Trump is like a relief pitcher coming in for the ninth inning with a score of 1-0, intentionally walking the based loaded, and touting his team’s lead to people who haven’t been watching.  We know that he is setting us up for a major setback, and he’s truly playing for the other team, the fossil fuel industry.  Perversely, he claims victory for emissions reductions that resulted from a switchover from coal to natural gas, when one of his top goals has been to save the coal industry.  More perversely, his speech claimed false progress on emissions, yet still has never conceded that climate change is a problem – it’s a delicate dance he does, with his pants on fire.

This discussion does raise the question of whether the US is already “doing its share” when it comes to reducing emissions.  If the emissions have been on the decline for the past decade, are we therefore doing a good job?  The answer is a resolute No – as the reductions have resulted predominantly from a shift from coal to natural gas, our energy and transportation infrastructure have not moved away from fossil fuels, and we have actually made very few of the difficult structural changes needed to put us on track for the 80-100% reductions in carbon emissions necessary to solve the problem.  As these reductions need to occur within a decade or two, the present moment is critical for aggressive changes that Obama sought to set into motion with his Clean Power Plan and automobile emissions reduction standards, both of which Trump has buried.

Nothing is more important than removing Trump from the pitcher’s mound before he causes irreparable damage to the livability of our planet for future generations.  The New York Times published a nice fact check article on his recent speech, but it only identifies his “misleading” explicit statements.

Let there be no doubt:  Trump’s is out testing the theme that he is helping fix the problem of climate change, and this is a Pants On Fire lie.

Posted in air pollution, climate | Tagged , , , , , , , , , | Comments Off on Pants on Fire, Causing Higher Carbon Emissions

Riding on Carousels and Ocean Gyres

Posted on June 2, 2018 by Philip Orton

I had a little fun Friday with a television expert appearance, helping people understand a little mystery – what might have happened to a real estate sign from New Jersey that was found on a French beach.  The story was mostly already formed, being in the news cycle for nearly a day already, but CBS New York just wanted to hear some expert opinion on the sign’s possible trek and the ocean science to explain it.

Never one to turn down an opportunity to get my little academic institution’s name in the news, I took on the treacherous task!

Image result for carousel asbury park

The sign was lost during Hurricane Sandy, and as it was made of plastic it floated flat just at the surface, making a perfect drifter to follow the ocean currents.  The main question Vanessa Murdoch had was:  Why would the sign take 5.5 years to cross the Atlantic?

The average flow of surface water in the world’s oceans is called the “wind-driven circulation”, and in the North Atlantic this is a clockwise circular pathway called a Gyre. Winds at our latitude tend to travel on average from west to east, whereas in the tropics north of the equator, the trade winds blow from east to west.  Add in Earth’s rotation (via the Coriolis Force) and you get a circulation pattern which is clockwise around the North Atlantic.

Of course, I pointed out that in Jersey Shore terminology, one might think of it as a Carousel or merry-go-round.  A ride around the gyre is known to take about 3.3 years – this stat comes from a fun oceanographer I’ve met before who is famous for tracking and studying floating ocean debris, Curtis Ebbesmeyer.

Nobody can know for certain the exact path followed by the sign, but if it hopped on this carousel and took this typical or average pathway and speed, we can say its likely that it completed one round trip — crossing the Atlantic and back again, and then back across!  In the 5.5 years since Sandy, there would be time for 1.5 trips around the carousel, or three Atlantic crossings.

The Gulf Stream is generally a very reliable current, though the rest of the gyre is less so — mariners discovered these currents centuries ago and often used them successfully for navigation.  That is because these gyre currents don’t rely on local weather and winds, they rely on large scale average weather, or climate, to drive them.

Read the story and see the news clip for yourself – http://newyork.cbslocal.com/2018/06/01/nj-sign-found-in-france-update/

 

Posted in urbanoceanographer, water, weather | Tagged , , , , , , , , , , | Comments Off on Riding on Carousels and Ocean Gyres

Repetitive Flooding Coming with Winter Storm Riley

Posted on March 1, 2018 by Philip Orton

Low-lying areas of the NYC Metro area should expect coastal flooding over multiple high tides Friday through Sunday, due to Winter Storm Riley’s winds coinciding with the month’s highest tides.  The forecast for coastal areas is significantly worse than for NY/NJ Harbor areas like Manhattan and Hoboken, so I’ll start with comments on these regions.  Consult the National Weather Service for official consensus guidance, but here I’ll summarize the picture from my perspective interpreting Stevens SFAS forecasts.

gfs_mslp_wind_neus_6

GFS weather model forecast for 7am EST Friday 2 March.  Lines show pressure isobars and wind speeds are colored by knots (scale on right). The storm continues to slowly move eastward from Saturday through Monday.

Areas like Keansburg, Sandy Hook and Jamaica Bay are all looking at moderate flooding and the outside chance of “major” coastal flooding.

sfas_plot-Inwood180301-0737

Stevens Flood Advisory System (SFAS) experimental forecast for water levels at Jamaica Bay’s Inwood, New York City (magenta), relative to NAVD88 (similar to mean sea level). Observed water levels are also shown (red dots), as well as 90% confidence intervals (grey shading).

Thus, there is a good chance of low-lying property flooding, and of water blocking streets and becoming trapped for some parts of the Rockaways and all the ‘usual’ locations (eg Broad Channel, Old Howard Beach), Friday through Sunday, peaking multiple times over several tidal cycles.  In Jamaica Bay, there is potential for a water level as high as 7 feet navd88, though the central estimate is 5.5 feet (moderately high uncertainty – whether the winds are north or northeast, basically).  The highest water level since Sandy was 5.7 feet navd88, and Sandy hit 10.5-11 ft navd88 there, for comparison.

New York /New Jersey Harbor is more likely to see “minor flood” levels, as shown below. The central estimate peak water levels of 5 feet navd88 translate to widespread nuisance flooding of streets and trapped rainfall which won’t drain due to sea levels blocking stormwater drainage.  These lower flood elevations in the harbor areas are expected because the winds will often be out of the north, or north-northeast, which is amenable to offshore surge (blame Earth’s rotation!), but actually blows out of NY/NJ Harbor locally.  However, there is about a 5% chance of seeing 6 ft navd88, which would become problematic at more locations, though still well below levels needed to cause widespread flooding.

sfas_plot-Battery180301-0737

Stevens Flood Advisory System (SFAS) experimental forecast for water levels at Battery Park, New York City (magenta), relative to NAVD88 (similar to mean sea level). Observed water levels are also shown (red dots), as well as 90% confidence intervals (grey shading).

The storm surge continues to roam around the 1-3 foot level all weekend due to the storm tracking offshore and then “bombing out” and sticking around.  Winds will continue from the north and northeast all weekend, pumping water into New York Bight and sending large waves toward the New Jersey and Mid-Atlantic coastlines.

gfs_mslp_wind_neus_11

GFS weather model forecast for 1pm EST Saturday 3 March.  Lines show pressure isobars and wind speeds are colored by knots (scale on right). The storm continues to slowly move eastward from Saturday through Monday.  The storm central pressure is forecast to be 972 mbar at this time, the forecast minimum (by GFS).

Tip of the hat to Nickitas Georgas and Alan Blumberg, now based at Jupiter Intel, who lead creation and development of the Stevens Flood Advisory System.  If you value the SFAS flood forecasts, as we all should (they define the state-of-the-art), you might contact them to inquire about the future of the system and its possible funding.

 

Posted in water, weather | Tagged , , , , , , , | Comments Off on Repetitive Flooding Coming with Winter Storm Riley

Investing in NOAA Ocean and Atmospheric Research

Posted on March 5, 2017 by Philip Orton

The Washington Post reported Friday that the Trump Administration is seeking huge cuts from the National Oceanic and Atmospheric Administration (NOAA) 2018 budget, including eliminating the Sea Grant Program and shaving 26% from the Office of Oceanic and Atmospheric Research (OAR).

My background is in studying the physics of the ocean, and my main area of research is coastal flood risk and mitigation.  Coming from a region that is still recovering from Hurricane Sandy, NYC’s largest flood in at least 300-years, I have some expertise on the return on investment of government funding under NOAA-OAR.  This funding enables research that has directly helped guide societal decisions that save money and make communities safer from extreme weather.

Among other things, OAR funds to the Climate Program Office have supported my research for the Consortium for Climate Risk in the Urban Northeast (CCRUN), under the Regional Integrated Sciences and Assessments program.  This funding enables our consortium of about ten lead scientists at six research institutions to study present and future risk from flooding, hurricanes, heat waves, drought, and other natural hazards.

This funding, typically below a hundred thousand dollars per year at each institution, can have huge economic benefits.  What people probably won’t realize from the headlines is that NOAA’s “climate” research, under the department of Commerce, is about both weather and climate risk, conducted arm-in-arm with governments and other stakeholders, and has a main goal of providing economic benefits.

For example, I just published a paper that quantified present-day coastal flood risk for the New York City region, a region with an annual economic output of about 1.5 trillion dollars in commerce.  Hurricane Sandy disabled this commercial capital for days and changed some people’s lives for years, with total damages at New York City alone of about $20 billion.  Nobody was adequately prepared for Sandy’s record-setting flood, which was far higher than anything in the prior century.

In the years before Sandy, CCRUN scientists were warning what could occur and how preparations and protections should be made.  During Sandy, CCRUN scientists were on blogs, television, making forecasts, helping explain what could occur, and demonstrably saving lives.

After Sandy, decisions had to be made quickly on what to do to prevent such devastation from occurring again.  But while FEMA’s work suggested a flood like Sandy’s could happen again soon, with a 10% chance of occurring within a decade, other studies suggested it was a much less likely event, with less than a 1% chance or less.  My recent published research has shown that the reality is likely in between the two results, has helped to reduce the uncertainty, and is now improving the basis on which multi-billion-dollar flood protection decisions are being made – I have met with or discussed these results many times with city planners and the director of New York City’s $20 billion flood mitigation plan.

Looking beyond present-day risks from extreme weather, climate change causing the planet and ocean to warm, and sea level is rising and accelerating.  NOAA funding sensibly enables scientists to evaluate how flood risks are growing and evaluate potential adaptation options that will save money, such as wetlands, levees or storm surge barriers.

Risk assessment builds the understanding of probabilities of damaging hazards, which enables successful decision-making.  On the heels of three straight temperature record-breaking years (2014, 2015, 2016) and three straight record-breaking decades (1980s, 1990s, 2000s), many in the Trump Administration are conceding that the planet is warming.  A sensible risk management approach will avoid severe cuts to NOAA-OAR, and enable scientists to seek to better understand the problem and help stakeholders prepare for its potential impacts.

Posted in climate, opinion, water, weather | Tagged , , , , , , , , , , , | Comments Off on Investing in NOAA Ocean and Atmospheric Research

A “new normal” or drowning by a million drops?

Posted on February 25, 2016 by Philip Orton

I was interviewed the other day on WNYC regarding flood events of the past few months — there is a concern that the three events that flooded some low-lying neighborhoods with roughly a foot of water signify a “new normal”, but what I’m seeing from the science and data is that we just had an unlucky few months where wind events coincided with the largest tides (spring tides).

Some think that the landscape was altered by Sandy and is leading to higher floods — I am skeptical that this has had any measurable effect.  Much like one recent study, we are evaluating whether the tide channels have changed by comparing pre-Sandy sea level data to post-Sandy data, but initial qualitative looks at the data suggest nothing abruptly changed in Jamaica Bay (or places to the east, where people are also concerned that there is “a new normal”).

In the longer-term, of course, Jamaica Bay’s inlet and channels are massively overdredged, and the recent flood was subtly AMPLIFIED (contrasting Sandy Hook and Jamaica Bay Inwood tide gauge peaks) going into the bay, whereas the shallower system of prior decades-to-centuries did not amplify flood levels. One recent research paper of ours addresses this in a very qualitative sense, but we are working on publishing some more detailed analyses comparing the 1880s landscape to the present-day, and how the present-day shipping channel amplifies flooding in the bay.

I also had a recent email exchange with NYC City Planning about whether we can measure compaction of land areas over 5-10 year periods using recent LIDAR data, but this withered and went silent recently.  It is possible that the heavy water from Sandy caused abrupt compaction in some landfilled neighborhoods, perhaps lowering land areas by many inches in one day.  That would lend credence to the claim that things have gotten worse for some locations.

Sea level rise has been about 4 inches in 25 years (10 cm), so is just a gradual change.  Actually the past few years had lower mean sea levels than the few years prior … there is year-to-year variability.  So there isn’t really a “new normal” for sea level rise, just a gradual drowning by a million drops.

Also, tides this year and in recent years and the near future are larger than normal by about an inch … there is a 19-year cycle set by the planes of the earth-moon orbit and earth-sun orbit that is at its peak right now.  So this is a minor factor, but one more …

Posted in climate, water, weather | Tagged , , , , , , , , , | 2 Comments

Nor’easter Flood Intermission and the Coming Second Act

Posted on January 23, 2016 by Philip Orton

As things have paused between high tides, we have a sort of intermission in the coastal flood stresses impacting many of us.  Water levels are on their way up again, and here’s an update on what happened and what I expect will happen through the remainder of the storm.  A big concern is obviously that this massive snowstorm could coincide with seawater flooding, and that we’ll have ice floes and water in our neighborhoods.

Major coastal flooding has already severely impacted some southern parts of NJ and states further south. Several neighborhoods there have seen floodwaters, but the worst flooding should be over; flood levels on the coming high tides are forecast to be lower.

All low-lying areas, as well as areas within the New Jersey back bays should remain vigilant over this evening’s high tides, as there is a chance they may experience worse conditions later on in the day.  I can’t make any blanket statements about all sites, as some have complex sea level patterns. However, the Stevens forecasts are available for a great many areas, so check them out.

Around the NY/NJ Metro area, moderate coastal flooding was observed in southern Raritan Bay, Upper East River and near Freeport NY.  Minor flooding was observed in several other places.

The forecasts provided by Stevens Institute, run every 6 hours, are experimental but can compliment NOAA forecasts, and have many additional features such as grey uncertainty errorbars (5th to 95th percentile estimates). This morning’s peak water levels were observed to reach the models’ higher uncertainty limits, but have remained within the range of those predictions.

So here is the good news:  Offshore winds have been dropping for a few hours now, and rotating to come from the north-northeast, and then north this evening or overnight.

As a result, the surge is also dropping.  Also, the evening high tide is a weaker high tide than the morning tide.  As a result, there is only a small likelihood of exceeding the water levels that occurred on the earlier high tide, for the entire region.  For the New York / New Jersey Metro area, at the very most they will only exceed them by roughly a half foot.

You can continue monitoring the observations and forecasts in www.stevens.edu/SFAS.

Posted in water, weather | Tagged , , , , , , , , , , , | Comments Off on Nor’easter Flood Intermission and the Coming Second Act

Nor’easter Jonas Evening Forecast Addendum

Posted on January 21, 2016 by SeaAndSkyNY

Additional details on the New York / New Jersey Metro Area

Getting it right with “minor” versus “moderate” flooding is particularly important when there is ice and freezing temperatures, as NOAA’s definitions (see below) suggest some evacuation may be needed when they designate flooding as moderate.

As mentioned in the prior post, areas in New York Harbor and up the Hudson like Hoboken, as well as the New Jersey Meadowlands have a good chance of minor flooding, but have a very low chance of moderate flooding.  However, some other parts of the Metro Area have a reasonable chance of “moderate flooding” like the New Jersey coast – sites that are close to the ocean, or in Newark Bay and Arthur Kill.  Examples are Jamaica Bay, Raritan Bay, the south end of Newark Bay, and Arthur Kill.  These areas are likely to have minor flooding and have a good chance (about as likely as not) to see moderate flooding levels (e.g. over 5.4 feet NAVD88 or 8.7 feet MLLW at Inwood, Jamaica Bay).  Detailed forecast plots for these sites are all available on the Stevens Flood Advisory System (http://stevens.edu/SFAS).

NOAA’s definitions for flooding are:

Minor Flooding – minimal or no property damage, but possibly some public threat (e.g., flooding of roads).

Moderate Flooding – some flooding of structures and roads near stream. Some evacuations of people and/or transfer of property to higher elevations.

Major Flooding – extensive flooding of structures and roads. Significant evacuations of people and/or transfer of property to higher elevations.

 

NY/NJ Snow Forecasts

The Global Forecast System (GFS) and ECMWF higher spatial resolution model (HRES) are both showing a range of approximately 4-10 inches of accumulated snow in the Northern parts of New Jersey and the New York City area.

The snow is to begin in the morning of Saturday, January 23 and the end of snow accumulation is expected around early Sunday morning (1:00 am – 5:00 am EST). The highest snow rates are expected on January 23 (between 6 pm and midnight EST) from what the models are showing.

The areas in Southern New Jersey and Trenton are more likely to receive up to 20 inches of snow based on the ECMWF model. However the GFS model is indicating an accumulated snow of 12-16 inches.

 

Posted in water, weather | Tagged , , , , , , , , , , , , | Comments Off on Nor’easter Jonas Evening Forecast Addendum